By Peter R. Mouton
—
For centuries dating back to ancient Greeks and Egyptian civilizations, humans have sought methods to quantify 3-D objects. Stereology, derived from the Greek stereos, is a coined term that refers to the analysis of objects in 3-D. Stereology as a scientific discipline did not exist until German-born histology Professor Hans Elias organized the first meeting in 1961.
For this small conference, Elias brought scientists from the fields of biology, geology, engineering, and materials sciences to the Feldberg, a mountaintop retreat in the Black Forest of Germany. The purpose of this gathering was to share and discuss approaches for quantifying 3-D objects based on their appearance on 2-D sections.
After a brief notice about the stereology meeting appeared in Science, Elias received phone calls and mail from scientists in academia, government agencies, and private industry requesting information about the next stereology meeting. The following year the International Society for Stereology (ISS) convened for its first congress in Vienna, Austria.
The ISS continues today with distinction as the largest multidisciplinary collaboration of international scientists with a non-war purpose in human history
The First Decade of Stereology (1961-1971)
The rise of stereology in the 1960s coincided with a number of technological innovations, including the availability of powerful yet affordable microscopes and novel histological procedures and immuno-based methods for visualization of specific microstructures. For the first time, biologists saw their tissues, cells, blood vessels, and other biological objects with unprecedented resolution and specificity.
Not surprisingly, this observations stimulated hypotheses and experiments with normal, diseased, and experimental groups that required reliable quantitative endpoints. These events contributed to a growing interest in quantitative morphometry in general, and especially the emerging field of stereology.
The Second Decade (1971-1981)
By the 1970s biologists began to favor the more objective stereology approaches over subjective evaluations by experts, that were well known to suffer from poor inter-rater reliability. Two peer-review journals, the Journal of Microscopy and Acta Stereologica (now Image Analysis & Stereology), took the lead in publishing peer-reviewed reports about stereology-based research.
By the mid 1970s mathematicians brought their unique perspectives to the theoretical aspects of stereology, and quickly identified a major flaw in earlier approaches that used Euclidean formulas based on classical shapes. Euclidean formulas apply only to objects that fit the classical models such as spheres, cubes, cylinders, e.g., volume of a sphere (V = (4/3) pi• r3).
Mathematicians pointed out that accurate quantification of biological structures, where essentially nothing fits these classical models, requires stochastic geometry and probability theory.
The Third Decade (1981-1991)
Following the disector principle by D.C. Sterio (1984), Gundersen and colleagues led the field with unbiased methods for Region Volume based on the Cavalieri method (Gundersen & Jensen, 1987), Number based on the director principle (Gundersen, 1986), Mean Object Volume using the Pappas-Guldinus (Gundersen and Jensen 1985, Gundersen, 1988), and Surface area (Baddeley et al., 1986).
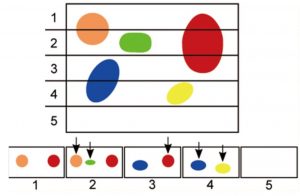
Figure 1: The counting of object of interest is dependent on orientation as exemplified by the Cavalieri principle.
By the end of the decade, design-based methods were developed for quantifying Object Length, the last of the four first-order parameters (Gokhale, 1990). Making unbiased stereology efficient enough for routine research studies followed soon thereafter with the advent of computers in the 1990s.
The Fourth Decade (1991-2001)
Several events contributed to a large spike in stereology-related papers in the scientific literature. Professional scientists with strong stereology training established annual workshops and courses on applications of unbiased stereology to biological systems. These courses taught scientists Ewald Weibel’s “Do More, Less Well” concept of increasing efficiency by sampling at the greatest sources of variation.
Second, editors of prestigious journals and grant reviewers began specifying their preferences for design-based stereology methods over assumption- and model-based (biased) approaches. For example, the following “Letter from the Editor” appeared in the Journal of Comparative Neurology [364(1), 6-15, 1996]:
“Stereologically based unbiased estimates are always preferable for establishing absolute counts or densities of structures in tissue sections. We expect that any papers that use simple profile counts, or assumption-based correction factors, will produce adequate justification for these methods. Referees are urged to insist on unbiased counts when [this justification] is not adequate.”
Clifford B. Saper, M.D., Ph.D.
Editor-in-Chief, JCN
Professor, Department of Neurology
Harvard Medical School
Boston, MA
Finally, collaborations between stereologists and computer engineers led to highly efficient computerized stereology systems that dramatically increased the speed of data collection over non-computerized methods.
The Fifth Decade (2001-2011)
The advent of stereology software allowed for analysis of tissue and images sliced at any orientation (Mouton et al., 2002; Gokhale et al., 2004). Workers in many disciplines expanded their use of fluorescence imaging and other microscopic approaches for visualization and quantification of microstructures using stereology approaches.
Several comprehensive textbooks were published with detailed procedures and practices with emphasis on biological applications (Mouton, 2002, 2011; Howard and Reed, 2005).
The Current Decade (2011-2021)
With strong support from the SBIR program of the NIH (U.S. Public Health Service), computerized stereology applications continue to minimize or eliminate the need for user-based data collection. Central to these novel approaches is the combination of unbiased stereology with technology for image segmentation and feature recognition based on size, staining, texture, shape, and other characteristics of biological microstructures (Mouton et al., 2005; Elozory et al., 2012; Chaudhury et al., 2013).
Systems will soon be available for accurate and highly efficient quantification of all first- and second-order stereology parameters and their variation with minimal “human-in-the-loop” interaction.
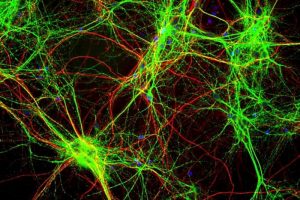
Figure 2: Deep learning facilitates the counting of cells, blue is the manually counted and red is the automatically counted cells.
Peter R. Mouton, Ph.D.
Professor of Stereology
Department of Pathology & Cell Biology
University of South Florida School of Medicine, Tampa, FL.
Chief Scientific Officer, Stereology Resource Center, Inc.
For comments, questions, and clarifications, please email peter@disector.com.
Works cited
Chaudhury, B., Phoulady, H.A., Goldgof, D., Hall, L.O., Mouton, P.R, Hakim, A., Siegel, E.M. An Ensemble Algorithm Framework for Automated Stereology of Cervical Cancer, Proceedings of the International Conference on Image Analysis and Processing (ICIAP), Springer (Berlin) Vol I, pp. 823-32, 2013.
Baddeley, AJ, Gundersen, HJG, and LM Cruz-Orive. Estimation of surface area from vertical sections. J. Microsc. 142: 259-276, 1986.
Elozory, D.T., Bonam, O.P., Kramer, K., Goldgof, D., Hall, L., Mangual, O., Mouton, P.R. Automatic Section Thickness Determination Using An Absolute Gradient Focus Function. J Microsc, 248(3): 245-59, 2012.
Gokhale A.M. Unbiased estimation of curve length in 3-D using vertical slices. J. Microsc. 159,133-41, 1990.
Gokhale AM, Evans RE, Mackes JL, Mouton PR. Stereological Estimation Of Surface Area In Thick Transparent Sections Of Arbitrary Orientation Using Virtual Cycloids. J Microsc 216(Pt1): 25-31, 2004.
Gundersen HJG, Jensen EB. Stereological estimation of the volume-weighted mean volume of arbitrary particles observed on random sections. Journal of Microscopy 158:127, 1985.
Gundersen HJG. Stereology of arbitrary particles. A review of unbiased number and size estimators and the presentation of some new ones, in the memory of William R. Thompson.
Journal of Microscopy 143:3, 1986
Gundersen HJG, Jensen EB. The efficiency of systematic sampling in stereology and its prediction. Journal of Microscopy 147:229, 1987.
Gundersen, HJG. The nucleator. Journal of Microscopy 151:3-21, 1988.
Howard, C. V., Reed, M. G. Unbiased Stereology, 2nd ed. Oxford: BIOS Scientific Publishers, 2005.
Mouton PR. Principles And Practices Of Unbiased Stereology: An Introduction For Bioscientists. The Johns Hopkins University Press, Baltimore, Maryland, 2002.
Mouton PR, Gokhale AM, Ward NL, West MJ. Stereological Length Estimation Using Spherical Probes. J Microsc 206: 54-64, 2002.
Mouton, P.R. Unbiased Stereology: A Concise Guide. The Johns Hopkins University Press, Baltimore, Maryland, 2011.
Mouton, P.R. (Editor), Neurostereology, Wiley-Blackwell Press, Boston, 280 pages, 2014.
Sterio, D.C. 1984. The unbiased estimation of number and sizes of arbitrary particles using the disector. Journal of Microscopy 134(2):127-136.